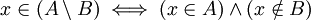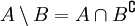El concepto de conjunto es intuitivo y podríamos definirlo simplemente como una colección de objetos, Usualmente los conjuntos se representan con una letra mayúscula: A, B, K,...
Llamaremos elemento, a cada uno de los objetos que forman parte de un conjunto, estos elementos tienen carácter individual, tienen cualidades que nos permiten diferenciarlos, y cada uno de ellos es único, no habiendo elementos duplicados o repetidos. Los representaremos con una letra minúscula: a, b, k,...
De esta manera, si  es un conjunto, y
es un conjunto, y  todos sus elementos, es común escribir:
todos sus elementos, es común escribir:
El universo de discurso, conjunto universal o referencial, que normalmente se denota por las letras U, V o E, es un conjunto cuyo objeto de estudio son los subconjuntos del mismo.
Existe además, un único conjunto que no tiene elementos al que se le llama conjunto vacío y que se denota por  . Es decir
. Es decir
La característica importante de este conjunto es que satisface todos los elementos posibles no están contenidos en él, es decir
 .
.
Unión:
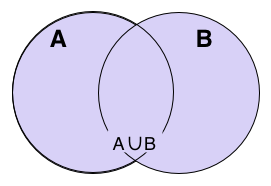
Para cada par de conjuntos A y B existe un conjunto que se denota como  el cual contiene todos los elementos de A y de B. De manera más general, para cada conjunto S existe otro conjunto denotado como
el cual contiene todos los elementos de A y de B. De manera más general, para cada conjunto S existe otro conjunto denotado como  de manera que sus elementos son todos los
de manera que sus elementos son todos los  tales que
tales que  . De esta manera
. De esta manera  es el caso especial donde
es el caso especial donde  .
.
Los elementos comunes a  y
y  forman un conjunto denominado intersección de
forman un conjunto denominado intersección de  y
y  , representado por
, representado por  . Es decir,
. Es decir,  es el conjunto que contiene a todos los elementos de A que al mismo tiempo están en B:
es el conjunto que contiene a todos los elementos de A que al mismo tiempo están en B:
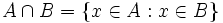 .
.
Si dos conjuntos  y
y  son tales que
son tales que 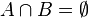 , entonces
, entonces  y
y  se dice que son conjuntos disjuntos.
se dice que son conjuntos disjuntos.
Los elementos de un conjunto  que no se encuentran en otro conjunto
que no se encuentran en otro conjunto  , forman otro conjunto llamado diferencia de
, forman otro conjunto llamado diferencia de  y
y  , representado por
, representado por  . Es decir:
. Es decir:
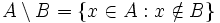 .
.
o dicho de otra manera:
Algunas personas prefieren denotar la diferencia de  y
y  como
como  .
.
Complemento
El complemento de un conjunto A, es el conjunto de los elementos que pertenecen a algún conjunto U pero no pertenecen a A, que lo representaremos por 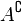 . Es decir
. Es decir
El conjunto complemento siempre lo es respecto al conjunto universal que estamos tratando, esto es, si hablamos de números enteros, y definimos el conjunto de los números pares, el conjunto complemento de los números pares, es el formado por los números no pares. Si estamos hablando de personas, y definimos el conjunto de las personas rubias, el conjunto complementario es el de las personas no rubias.
En vista de que  y
y  , entonces
, entonces
 ,
,
de manera que
Grafo
Un grafo es una pareja de conjuntos G = (V,A), donde V es el conjunto de vértices, y A es el conjunto de aristas, este último es un conjunto de subconjuntos de la forma (u,v) tal que
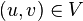 , tal que
, tal que  . Para simplificar, notaremos la arista {a,b} como ab.
. Para simplificar, notaremos la arista {a,b} como ab.Un vértice es la unidad fundamental de la que están formados los grafos. Los vértices son tratados como un objeto indivisible y sin propiedades, aunque puedan tener una estructura adicional dependiendo de la aplicación por la cual se usa el grafo; por ejemplo, una red semántica es un grafo en donde los vértices representan conceptos o clases de objetos.
tipos de Grafos:
Grafos Ciclicos
Un grafo ciclico consiste en un sólo ciclo. un grafo ciclico se denota por Cn, donde n es el número de vértices.
de vértices.
Grafos Bipartitos
Un grafo G es bipartito si puede expresarse como  (es decir, la unión de
(es decir, la unión de
dos grupos de vértices), bajo las siguientes condiciones:
- V1 y V2 son disjuntos y no vacíos.
- Cada arista de A une un vértice de V1 con uno de V2.
- No existen aristas uniendo dos elementos de V1; análogamente para V2.
Grafos Completos
Un grafo simple es completo si existen aristas uniendo todos los pares posibles de vértices.El conjunto de los grafos completos es denominado usualmente
 , siendo
, siendo  el grafo completo de n vértices.
el grafo completo de n vértices. Un Kn, es decir, grafo completo de n vértices tiene exactamente 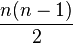 aristas.
aristas.
Árbol
Un árbol es un grafo dirigido aciclico en el que cada nodo está conectado con un camino simple, partiendo desde el nodo distinguido llamado "raiz". un nodo y es "hijo" de x, y x el "padre" de y, si y es es adyacente y x esta más cercano a la raiz o es la raiz.


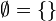


 y
y